Simple and best practice solution for (2xy)dy(x^2y^21)dx=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve it Equation SOLVE Solution for (2xy)dy(x^2y^21)dx We can rearrange this Differential Equation as follows dy dx = − x2 y2 x2 − xy = − ( 1 x2)(x2 y2) ( 1 x2)(x2 −xy) = − 1 ( y x)2 1 − y x So Let us try a substitution, Let v = y x ⇒ y = vx Then dy dx = v x dv dx And substituting into the above DE, to eliminate yHelp is appreciated Edit

Y Xy 1 Dx X 1 Xy X 2 Y 2 Dy 0
Solve y(2x^2-xy+1)dx+(x-y)dy=0
Solve y(2x^2-xy+1)dx+(x-y)dy=0-Contenido Tema 02 2 Ecuacionesdiferencialesdeprimerorden 21 Variablesseparables 22 Ecuacionesexactas 23 Ecuacioneslineales 24 Solucionesporsustitución Find dy/dx in terms of x and y, and thus find the coordinates of the points on C where dy/dx = 0 Start by differentiating x 2 – 3xy – 4y 2 64 = 0 with respect to x to obtain an equation in x, y and dy/dxY^2dx (x^2xyy^2)dy = 0 dy/dx = y^2/(x^2xyy^2)(1) Let y = vx dy/dx = v1 xdv/dx On putting dy/dx= vxdv/dx in eq(1) vxdv/dx= v^2x^ An equation in differential form M ( x, y) dx N (x, y



Find The General Solution Of Differential Equation 1 X 2 1 Y Dx Xy 1 Y Dy Sarthaks Econnect Largest Online Education Community
(x y 1)dx (x 4y 1)dy= 0 Solution 3 La encuaci on se transforma en la siguiente dy dx = y x 1 x 4y 1 (1) y realizamos el cambio de variable V = x y Por tanto tenemos que dy dx = 1 dV dx y la ecuaci on queda de la siguiente forma 1 dV dx = 2V 4 V 10 que simpli cada resulta dV dx = 3V 6Exercise 1 Standard form P(x,y)dxQ(x,y)dy = 0 ie P(x,y) = − y x2 and Q(x,y) = 1 x Equation is exact if ∂P ∂y = ∂Q ∂x Check ∂P ∂y = − 1 x2 = ∂Q ∂x ∴ ode is exact Since equation exact, u(x,y) exists such that du = ∂u ∂x dx ∂u ∂y dy = P dxQdy = 0 and equation has solution u = C, C = constant Toc JJ II J I Help a stranger please This is for my homework and I'm having a hard time solving these equations Show the complete solutions and final answers please It will be a great help Thank you so much This covers Additional Topics on Equations of Order One, Coefficient Linear in Two Variables 1 (6x3y2)dx(2xy1)dy=0 2 (x2y1)dx(2xy5)dy=0
An ordinary differential equation of first order and first degree can be written as dy dx = f(x,y) d y d x = f ( x, y) , where f(x,y) f ( x, y) is a function of two variables x,y x, y Which can(y^22xy)dx (x^2) dy = 0 Integrating factor y^2 solution xx^2/y = C Finding the integrating factor Giving these things some names names M(x,y) = y^22xy N(x,y) = x^2 M(x,y) dx N(x,y) = 0 We're looking to make this an exact equation, because if we do, it can be solved rather systematically In order to be exact, by claurait's theoem (think that's the name of Homework Statement Solve (xy1)dx(yx5)dy=0 Homework Equations The Attempt at a Solution x=uh y=vk Therefore h=2 and k=3 Therefore (uv)du(vu)dv=0 \\frac{dv}{du}=\\frac{uv}{uv} This is where I'm stuck I can't solve the equation above I have a
Theory Roots of a product 51 A product of several terms equals zero When a product of two or more terms equals zero, then at least one of the terms must be zero We shall now solve each term = 0 separately In other words, we are going to solve as many equations as there are terms in the product Any solution of term = 0 solves productSolution for Find the solution of the Differential Equation y(2x^2 xy 1)dx (x y)dy=0Popular Problems Calculus Find dy/dx 2xyy^2=1 2xy − y2 = 1 2 x y y 2 = 1 Differentiate both sides of the equation d dx (2xy−y2) = d dx (1) d d x ( 2 x y y 2) = d d x ( 1) Differentiate the left side of the equation Tap for more steps By the Sum Rule, the derivative of 2 x y − y 2 2 x y y 2 with respect to x x is d d x 2




Example 17 Show 2y E X Y Dx Y 2x Ex Y Dy 0 Particular




Ex 9 5 11 Find Particular Solution X Y Dy X Y Dx 0
can you please explain how to to find dy/dx for the function x^2 y Y^2 x = 2 asked in CALCULUS by mathgirl Apprentice differentiation;Learn how to solve differential equations problems step by step online Solve the differential equation xy*dx(1x^2)dy=0 Grouping the terms of the differential equation Group the terms of the differential equation Move the terms of the y variable to the left side, and the terms of the x variable to the right side Simplify the expression \frac{1}{y}dy Integrate both sides of theSolve the given initialvalue problem (xy)^2dx (2xyx^21)dy=0, y(1)=1 Best Answer This is the best answer based on feedback and ratings 92% (13 ratings) Given a differential equation of the form Mdx Ndy = 0 it's exact if Nx = My then to solve it we know that there is a solution F(x,y




What Is The Solution For Math Sqrt 1 X 2 Sqrt 1 Y 2 Dx Xy Dy 0 Math Quora
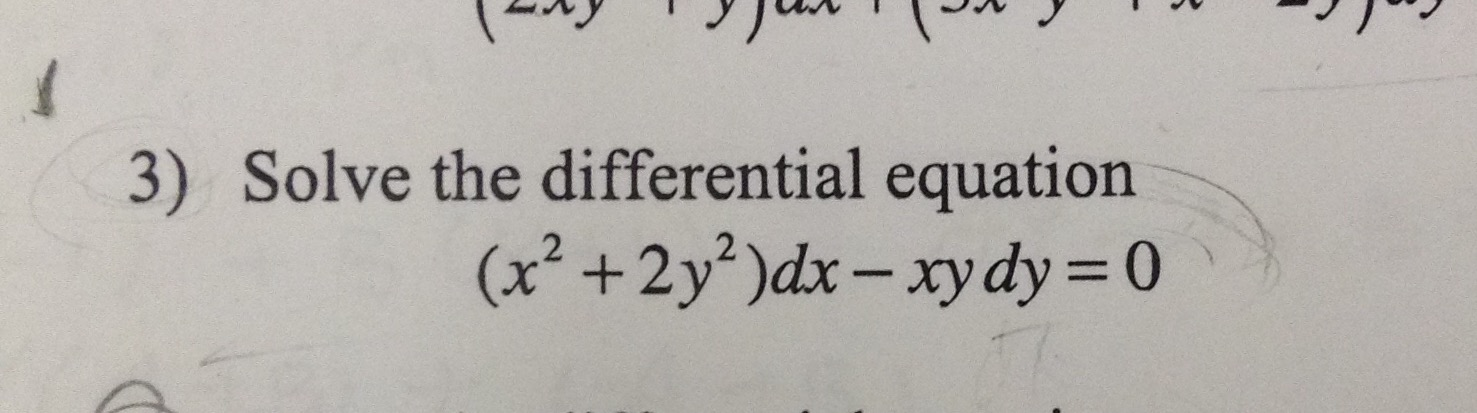



3 Solve The Differential Equation X 2 2y 2 Dx Xy Chegg Com
Click here👆to get an answer to your question ️ Solve (3xy y^2)dx (x^2 xy) dy = 0 , y(1) = 1 Join / Login > 12th > Maths > Differential Equations > Solving Homogeneous Differential Equation The solution of x 2 d x d y − x y = 1 cos x yFactor out the Greatest Common Factor (GCF), 'dy' dy(2x 1x 2 y 2x 3 1y) = 0 Subproblem 1 Set the factor 'dy' equal to zero and attempt to solve Simplifying dy = 0 Solving dy = 0 Move all terms containing d to the left, all other terms to the right Simplifying dy = 0 The solution to this equation could not be determinedWe evaluate the partial derivatives to check for exactness ∂M∂y = 9x 2 y 2;




X 2 Y 2 Dx 2xy Dy 0 Integrating Factor Novocom Top




Solve Y 2 2x 2y Dx 2x 3 Xy Dy 0 Mathematics Stack Exchange
Example 1 Solve (3x 2 y 3 − 5x 4) dx (y 3x 3 y 2) dy = 0 In this case we have M(x, y) = 3x 2 y 3 − 5x 4;Answered Solved Solve differential equation y(2x2xy1)dx(xy)dy=0(b) 2 x y dx ( y 2 x 2) dy = 0 Here, M = 2 x y, M y = 2x, N = y 2 x 2, and N x = 2 xNow, ( N x M y) / M = ( 2 x 2 x ) / ( 2 x y) = 2 / yThus, μ = exp ( ∫ 2 dy / y ) = y2 is an integrating factor The transformed equation is ( 2 x / y ) dx ( 1 x 2 y2) dy = 0 Let m = 2 x / y, and n = 1 x 2 y2Then, m y = 2 x y2 = n x, and the new differential equation is exact




Determination Of Integrating Factors Y Y 2x 2 Dx Chegg Com




Y Xy 1 Dx X 1 Xy X 2 Y 2 Dy 0
Set u = x y Hence d u d x = x d y d x y Hence your equation became x u d u d x − 1 = 1 2 u u − 1 u − 1 3 u 2 d u = 1 x d x Now you can integrate both sides You can then integrate both sides To write this as a fuction of y requires the Lambert W function I(X 2y) Dx − (2x − Y) Dy = 0 Department of PreUniversity Education, Karnataka PUC Karnataka Science Class 12 Textbook Solutions Important Solutions 984 Question Bank Solutions Concept Notes & Videos 470 Syllabus Advertisement Remove all ads (X 2y) Dx − (2x − Y) Dy = 0 Mathematics91 A product of several terms equals zero When a product of two or more terms equals zero, then at least one of the terms must be zero We shall now solve each term = 0 separately In other words, we are going to solve as many equations as there are terms in the product Any solution of term = 0 solves product = 0 as well




Engineering Mathematics Notes




Dx X Y 1 Dy 0 Novocom Top
Get an answer for 'solve first grade ecuation with bernoulli dy/dx = (y^22xy)/x^2 general ecuation and particular when y(1)=1' and find homework help for other Math questions at eNotesMath2xy\frac{dy}{dx}y^22x = 0/math math⇒ 2xy\frac{dy}{dx}y^2 = 2x/math math⇒ \frac{d}{dx}xy^2 = 2x/math math⇒ xy^2 = \int_{}^{}2x\ dx/mathCalculus Find dy/dx y^2=1/ (1x^2) y2 = 1 1 − x2 y 2 = 1 1 x 2 Differentiate both sides of the equation d dx (y2) = d dx ( 1 1−x2) d d x ( y 2) = d d x ( 1 1 x 2) Differentiate the left side of the equation Tap for more steps




The Solution Of The Differential Equation Y Xy 2x 2y 2 Dx X Xy X 2y 2 Dy 0 Is Given Youtube




1 X 2 Dy Dx Xy 1 Youtube
Test whether the differential equation is exact or not and solve it (x^4 y^4) dx − xy^3 dy = 0 asked Mar 17 in Mathematics by Mohsin Al Mamun (0 points) 0 votes 1 answer Integrating factor of the differential equation (1 – x^2) dy/dx − xy = 1 is asked in Mathematics by AsutoshSahni (526k points) differentialY (2x^2xy1) dx (xy) dy = 0 Using Type 6,determination of integrating factors Show the ExactEquation Using Type 6,determination of integrating factorsRewrite 2xy dxx2 dy−1 dy = 0 2 x y d x x 2 d y − 1 d y = 0 Change the sides $$2 xy \ dx x^2 \ dy = 1 \ See full answer below




Integrating Factors Found By Formula 11 Y Y 2x Chegg Com



1
You can separate it out as x d x y d y = x 2 − 1 y 2 1 now put y 2 1 = u and then continue to get a very simple integrable function 21(xy^2x)dx(yx^2y)dy=0 2 1 ( x y 2 x ) d x ( y − x 2 y ) d y = 0 or if you want y to be the independent variable dsolve ('Dx = (x*log (y)1/y)/ (y*log (y)exp (x*y))','y') However, there is no guarantee that 'dsolve' would succeed in finding an explicit solution If not, you would need to solve it numerically using specified initial conditions with one of the ode functions, such as ode45, ode23, ode113They are the same!



Find The Particular Solution Of The Differential Equation X 2dy Dx Xy 1 Cos Y X X 0 When X 1 Y Pi 2 Sarthaks Econnect Largest Online Education Community




Ex 9 5 12 Find Particular Solution X2 Dy Xy Y2 Dx 0
The Solution Of 1 X 2 Dy Dx 2xy Xsqrt 1 X 2 0 Is A Y 1 X 2 X y 2 dx 2xy x 21 dy 0 y 1 1 X y 2 dx 2xy x 21 dy 0 y 1 1Help is appreciated EditFind the particular solution of the differential equation (1 – y^2) (1 log x) dx 2xy dy = 0, given that y = 0 when x = 1 CBSE CBSE (Commerce) Class 12 Question Papers 1786 Textbook SolutionsY 2x 2 Xy 1 Dx X Y Dy 0 solve x 1 x 3 greater than 3 sony tc k555esg sony wf 1000xm3 true wireless earbuds review solve graphically 2x y 2 2y x 4 so nice to hear from you sony cfs 1065s sony wf 1000xm3 ペアリング iphone sony wf 1000xm3 ケースCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history




Solve 1 E X Y Dx E X Y 1 X Y Dy 0 Novocom Top
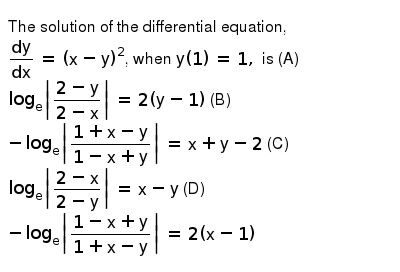



The Solution Of The Differential Equation Dy Dx X Y 2 When Y 1 1 Is A Log E Abs 2 Y 2 X 2 Y 1 B Log E Abs 1 X Y 1 X Y X Y 2 C Log E Abs 2 X 2 Y X Y D Log E Abs 1 X Y 1 X Y 2 X 1
2xy dx (x^2 1) dy =0 => 2xydx = (x^2–1)dy => 2x/(x^2–1)dx = dy/y after integrating both sides => ln(x^2–1) = ln(y) constant => ln(x^2–1)ln(y Verify that y = e^(m cos^(1)) x is a solution of the differential equation (1 x^2)d^2 y/dx^2 x(dy/dx) m^2y = 0 asked May 10 in Differential Equations by Yajna ( 299k points) differential equations y = (xlnx)/(1lnx) We have dy/dx = (x^2y^2xy)/x^2 with y(1)=0 Which is a First Order Nonlinear Ordinary Differential Equation Let us attempt a substitution of the form y = vx Differentiating wrt x and applying the product rule, we get dy/dx = v x(dv)/dx Substituting into the initial ODE we get v x(dv)/dx = (x^2(vx)^2x(vx))/x^2 Then assuming that x ne 0 this




Ex 9 5 15 Class 12 Find Solution 2xy Y 2 2x 2 Dy Dx 0 When



How To Solve Following By Variable Separation Method X 2 1 Y 2 1 Dx Xydy 0 Quora
24 #1 find the general solution of (y 1)dx(4x−y)dy = 0 then i put in standard form dx dy 4x 1y = y y 1 now im stuck i know the integrating factor is (1 y)4 which i multiply the equation withSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more∂N∂x = 9x 2 y 2;




Show That The General Solution Of The Differential Equation Dy Dx Y 2 Y 1 X 2 X 1 0 Is Given By X Y 1 A 1 X Y 2xy Where A Is Parameter Mathematics Shaalaa Com
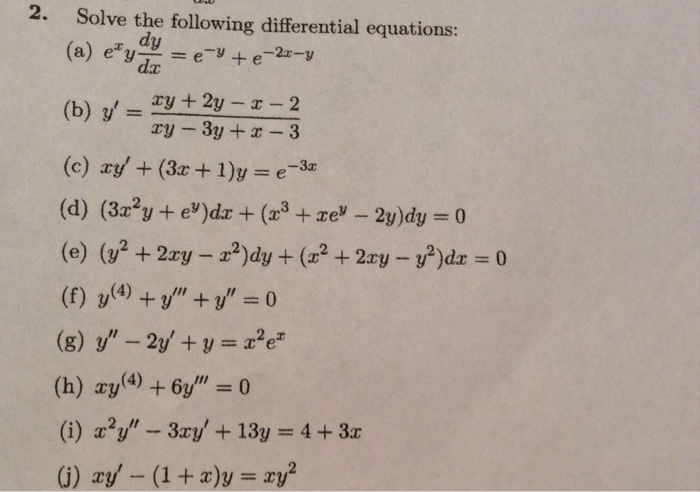



Solve The Following Differential Equation E Xy Dy Dx Chegg Com
Simple and best practice solution for y(xy1)dx(x2y)dy=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve itN(x, y) = y 3x 3 y 2;(3 x 2 y 2 xy y 3) dx (x 2 y 2) dy = 0 C Show that μ (x, y) is an Integrating factor for each non exact ODE and after multiplying by μ find solution 1 x 2 y 3 x (1 y 2) y 0 = 0, μ (x, y) = 1 xy 3 2 sin y y2 ex sin x dx cos y 2 ex cos x y dy = 0, μ (x, y) = ye x 3 3 x 6 y x 2 y 3 y x dy dx = 0, μ (x, y) = xy
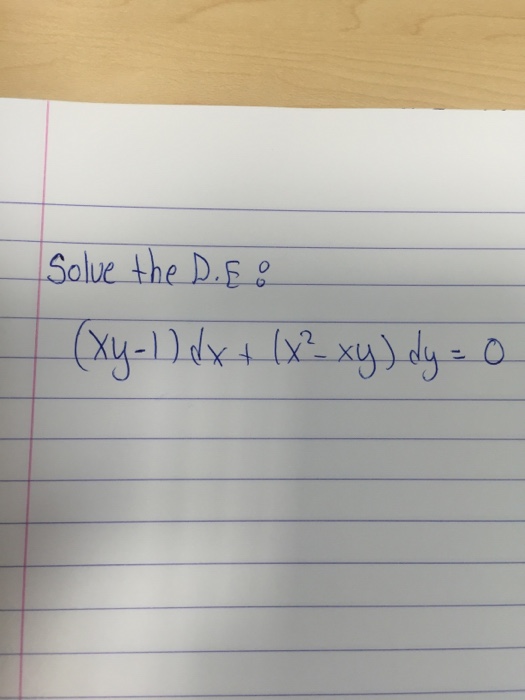



Solve The D E Xy 1 Dx X 2 Xy Dy 0 Chegg Com




Engineering Mathematics Notes
Re (3x5y)dx (xy) dy = 0 It's a differential equation Write it in the form of dy/dx y = x Then solve like a first order linear differential equation Edit tried to rewrite and solve it, but it's a nonlinear differential equation My abilities unfortunately only include linear ones with constant coefficients Example 17 Show that the differential equation 2𝑦𝑒^(𝑥/𝑦) 𝑑𝑥(𝑦−2𝑥𝑒^(𝑥/𝑦) )𝑑𝑦=0 is homogeneous and find its particular solution , given that, 𝑥=0 when 𝑦=1 2𝑦𝑒^(𝑥/𝑦) 𝑑𝑥(𝑦−2𝑥𝑒^(𝑥/𝑦) )𝑑𝑦 = 0 Step 1 Find 𝑑𝑥/𝑑𝑦Y' 5 y = 0 The highest order derivative present in the given differential equation is y' and index of its highest power is one ∴ the given differential equation is of order 1 and degree 1




The General Solution Of The Differential Equation Y 2 X 3 Dx Xydy 0 X 0 Is Brainiak




Consider The Differential Equation Xy 2 Bx 2y Dx Chegg Com
But if I expand the bracket $(xy)^2$ before integrating I will get $$\varnothing_1=\int Mdx=\int (xy)^2dx=\int (x^22xyy^2)dx=\frac{x^3}{3}xy^2x^2y$$ Wich will lead to the solution $$\varnothing=\varnothing_1\varnothing_2=\frac{x^3}{3}xy^2x^2yy=Constant$$ What is the wrong step ?For each of the differential equations given in exercise 1 to 1 2,find the general solution 1 d x d y 2 y = sin x 2 d x d y 3 y = e − 2 x 3 d x d y x y = x 2 4 d x d y sec= tan x (0 ≤ x ≤ 2 π ) 5 cos 2 x d x d y y = tan x (0 ≤ x ≤ 2 πCalculadoras gratuitas paso por paso para álgebra, Trigonometría y cálculo This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy Learn more Accept Soluciones (y1)^{2}dx=0 es Related Symbolab blog posts Practice, practice, practice Math can be an intimidating subject




Engineering Mathematics Notes
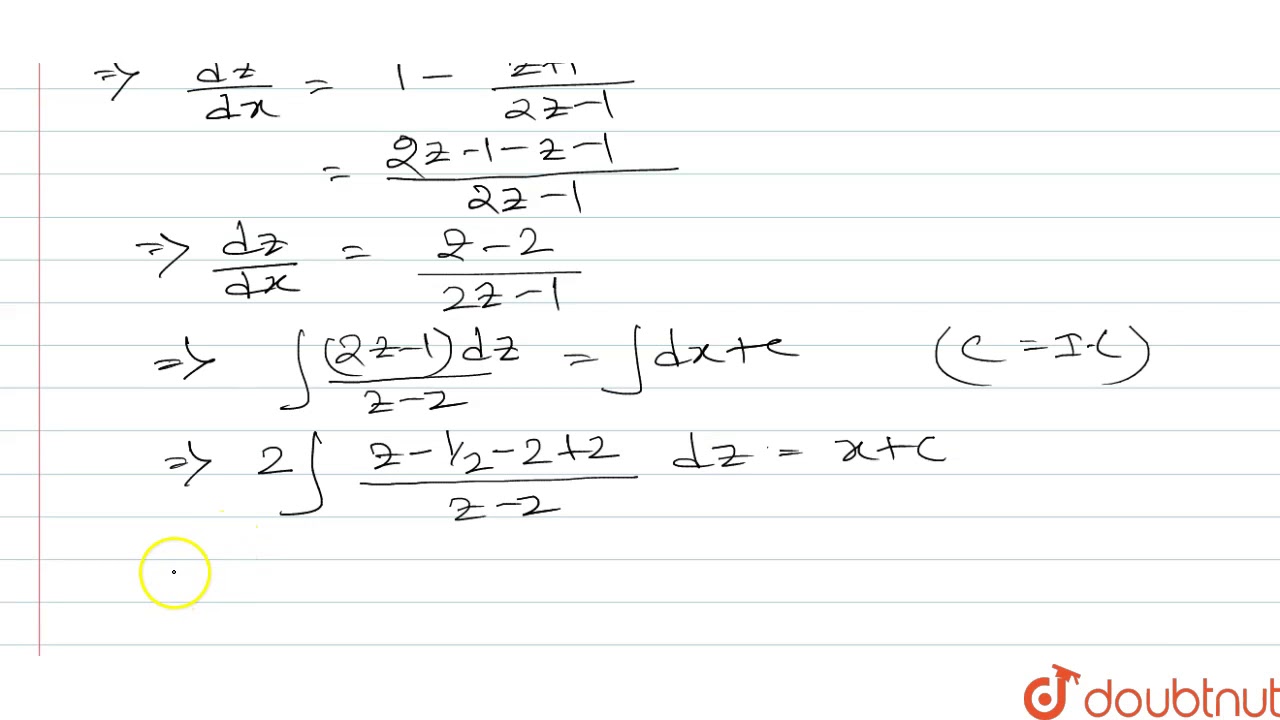



X Y 1 Dx 2x 2y 1 Dy 0 Youtube




In Solve The Given Initial Value Problem X Y 2 Chegg Com



Find The Particular Solution Of The Differential Equation 3xy Y 2 Dx X 2 Xy Dy 0 For X 1 Y 1 Sarthaks Econnect Largest Online Education Community



What Is The General Solution Of The Ydx Xy 2 X Y Dy 0 Quora




Engineering Mathematics Notes




Solve Y 2 2x 2y Dx 2x 3 Xy Dy 0 Mathematics Stack Exchange




Solve X Y 1 Dx 2x 2y 3 Dy 0 Youtube



How To Solve 2x Y 1 Dx X 4y 3 Dy 0 Quora




Math 432 Hw 2 5 Solutions Frostburg
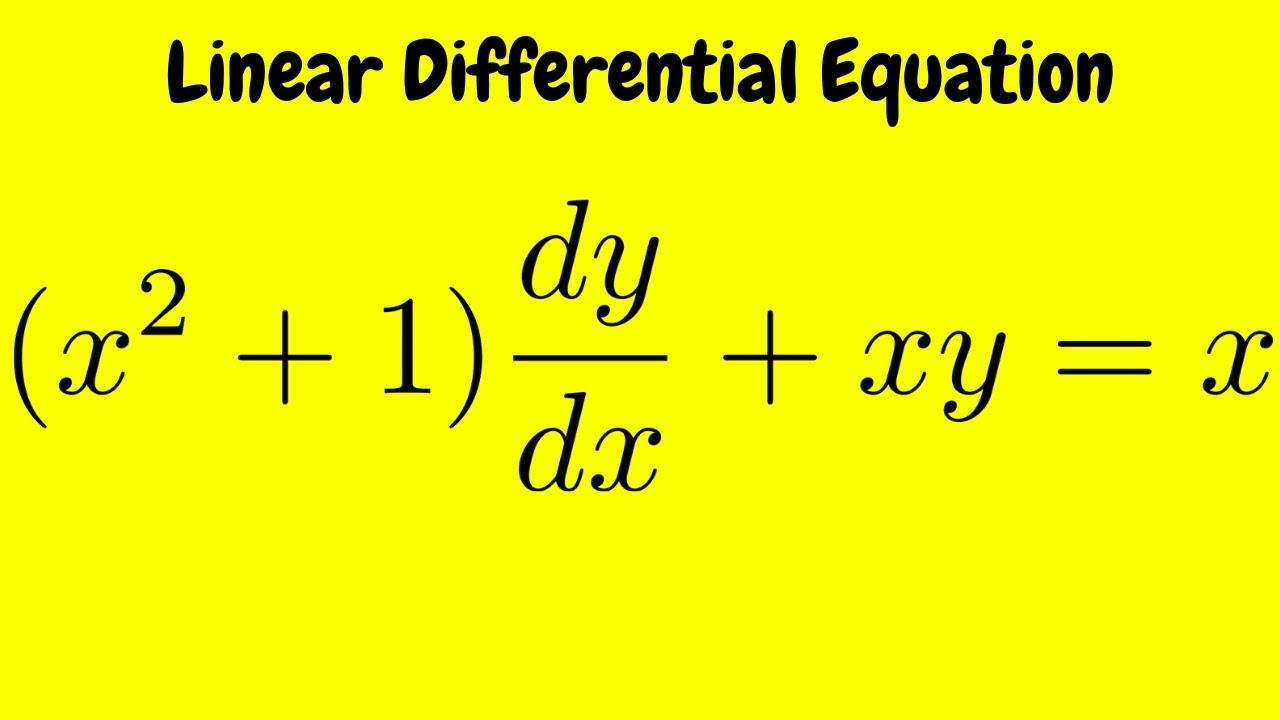



Solve The Linear Differential Equation X 2 1 Dy Dx Xy X Youtube



Solve The Following Differential Equation 1 X 2 Y 2 X 2y 2 Xy Dy Dx 0 Sarthaks Econnect Largest Online Education Community




Solve The Given Non Exact De Y 2x Y 1 Dx Chegg Com
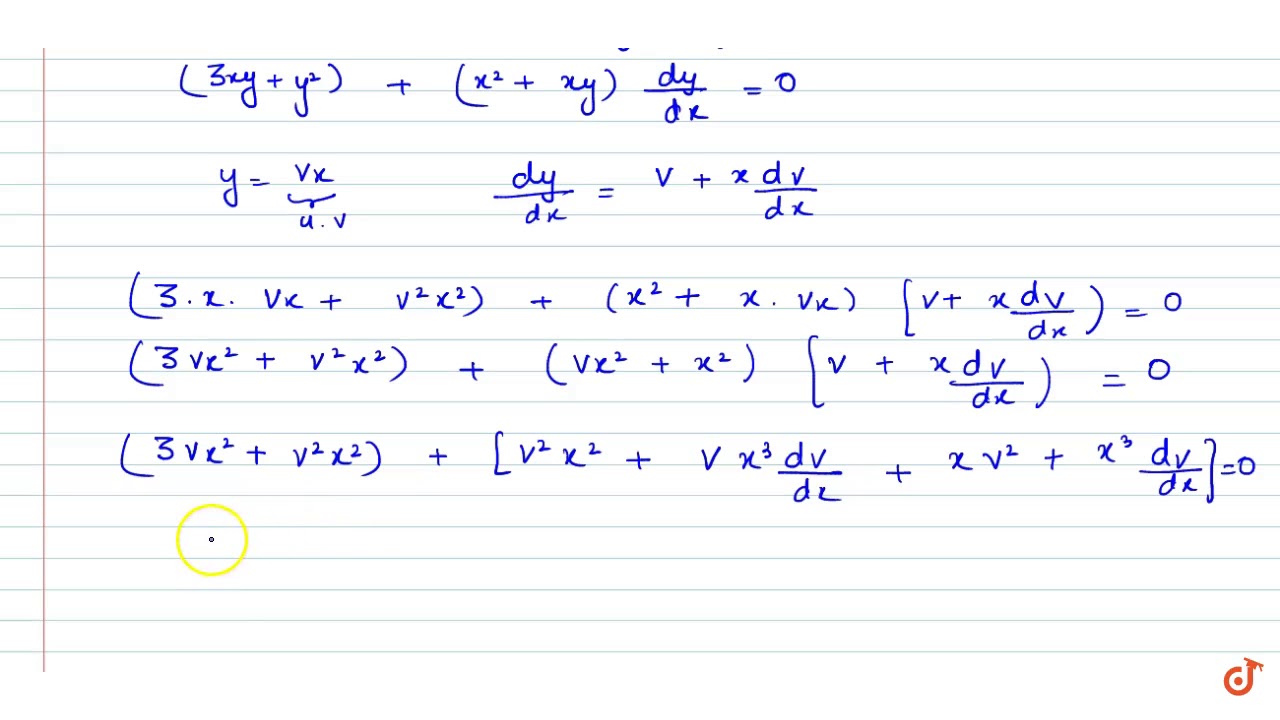



3x Y Y 2 Dx X 2 X Y Dy 0 Youtube
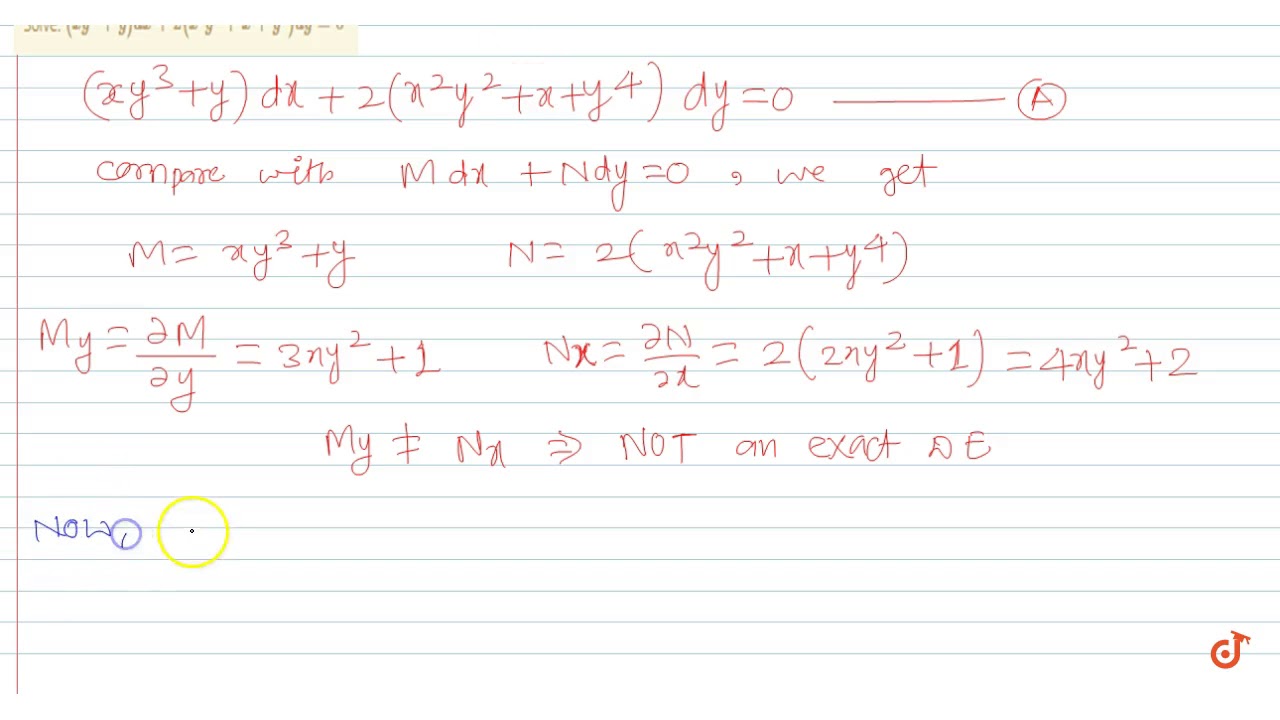



Solve Xy 3 Y Dx 2 X 2y 2 X Y 4 Dy 0 Youtube




Dy Dx X Y 1 X Y 3 Novocom Top




Solve The Differential Equation Dy Dx Xy 2 1 Chegg Com




15 2xy Y 2 Dx 2xy X 2 2x 2y 2 2xy 3 Dy 0 Homeworklib



Find The General Solution Of Differential Equation 1 X 2 1 Y Dx Xy 1 Y Dy Sarthaks Econnect Largest Online Education Community




First Order Differential Equations Ppt Download




For Problems 26 Determine An Integrating Factor Chegg Com




Solve The Given Differentia By Separation Of Chegg Com




1 9 Fghbhj Equations Function Mathematics




How To Solve 3xy Y 2 Dx X 2 Xy Dy 0 Also I Wish To Knw When To Use Y Vx Or X Vy Mathematics Topperlearning Com H9faf2xx



How To Solve For The General Solution Of The Following Differential Equation X 2 Y 2 1 Dx X X 2y Dy 0 Using An Integrating Factor Quora



How To Solve X Y 1 Dy X Y 1 Dx Quora




I 2x Y 1 Dx Ydy 0 Ii Xydx X2 Y2 Dy 0 Chegg Com



How To Solve Y X Y Dx X X Y Dy 0 Quora




Solve Each Differential Equation 1 X Dy Y 2 Dx Chegg Com




Engineering Mathematics Notes




Y 2 X 2 Dy Dx Xy Dy Dx Youtube




Y 2x Xy 1 Dx X Y Dy 0 Brainly In
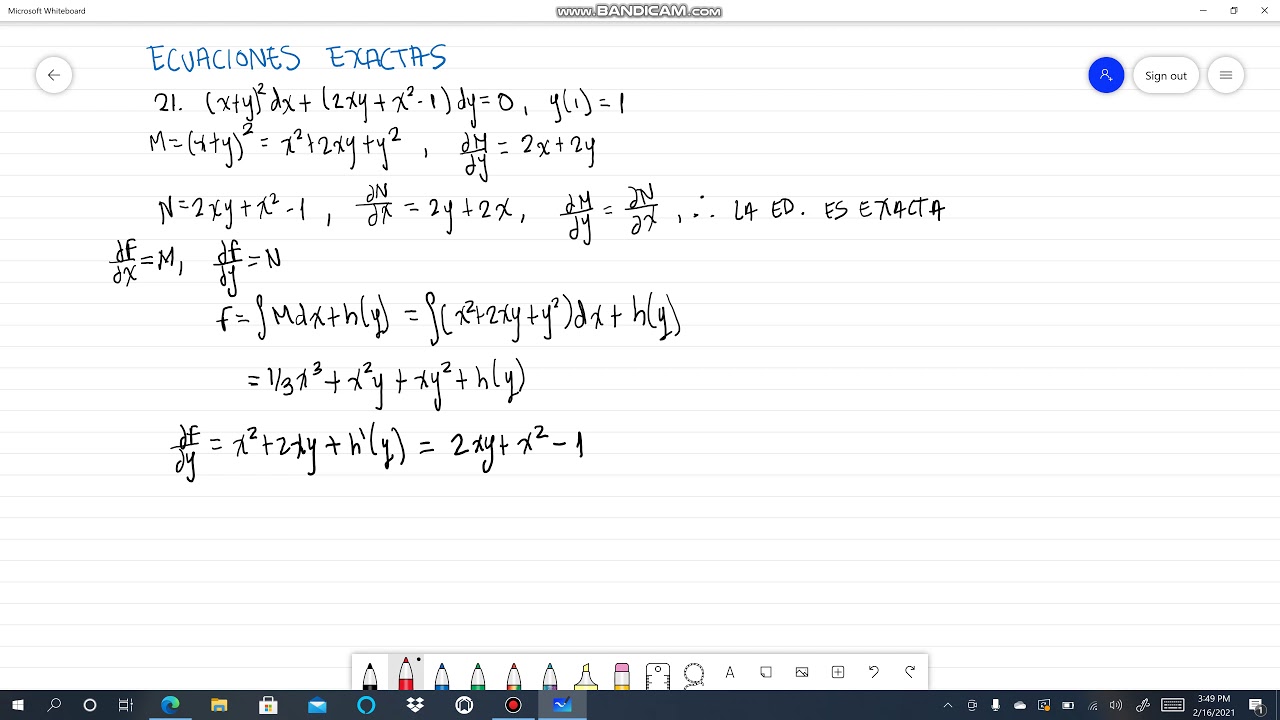



21 X Y 2 Dx 2xy X 2 1 Dy 0 Y 1 1 Ecuaciones Exactas Alexander Estrada Youtube




Differential Equations With Boundary Value Problems 9th Edition By Zill Solution Manual Download By Mydexher Issuu




Dy Dx X Y 1 X Y 3 Novocom Top



Solve The Following Differential Equation 1 X 2 Y 2 X 2y 2 Xydy Dx 0 Sarthaks Econnect Largest Online Education Community




Ipe Material Notes




Y 2x 3 Dx X 1 Xy Dy 0 Brainly In
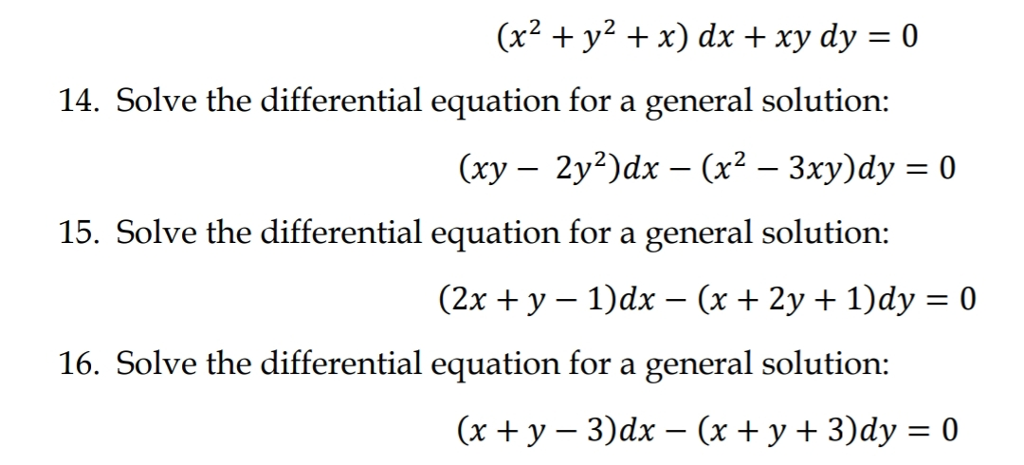



X2 Y2 X Dx Xy Dy 0 14 Solve The Differential Chegg Com




Math 432 Hw 2 5 Solutions




Y 2xy E X Dx E Xdy 0 Novocom Top




1 2e X Y Dx 2e X Y 1 X Y Dy 0 Novocom Top




How To Solve Show The Differential Equations Are Exact 2xy Y Tany Dx X 2 X Tany 2 Secy 2 2 Dy 0 Te Tx 2x Dx Dt Xe Xt 0 Quora
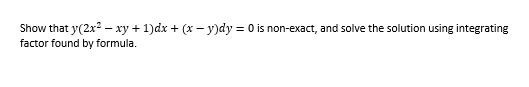



Show That Y 2x2 Xy 1 Dx X Y Dy 0 Is Chegg Com



What Is The Answer To These X Y Dx X Y Dy Quora



Solved Solving Exact First Oder Differential Equations 2xydx X 2 Cosy Dy 0 Y Xy 2 1 1 X 2y 2x Y Dx X 3y Dy 0 2x Y 4 Dx X 3y 12 Dy 0 Ye X S Course Hero



Q Tbn And9gcqqdjererih8cbajqv Puntih4ikbw7iy9bdv7cgyhxgixkwubp Usqp Cau
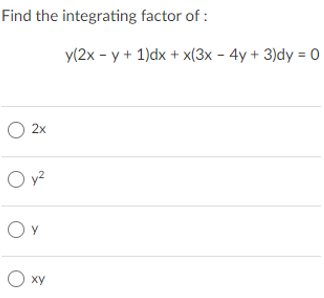



Answered Find The Integrating Factor Of Y 2x Bartleby



1




X Y 1 0 X Y 1 0 Solution Novocom Top



Solve X2 Dy Dx X2 Xy Y2 Studyrankersonline




Solved Problems In Differential Equations 2500 Solved Problems In Differential Docsity




Solve Y 2 2x 2y Dx 2x 3 Xy Dy 0 Mathematics Stack Exchange



Www Tau Ac Il Levant Ode Solution 6 Pdf



Solved Solve The Following Differential Equations X Y 3 Dx X Y 1 Dy 0 2 X Y 1 Dx 3x 4y 2 Dy C 3 1 Y 2 Xy 2 Dx X 2y Y 2xy Dy Course Hero




Solution Solve The Differential Equation X Y 1 Dx X 1 Dy 0 If




Xy X 2y 1 0 Novocom Top




2 Find The Complete Solution Of X 2 Xy Y 2 Dx Xy Dy 0 Youtube
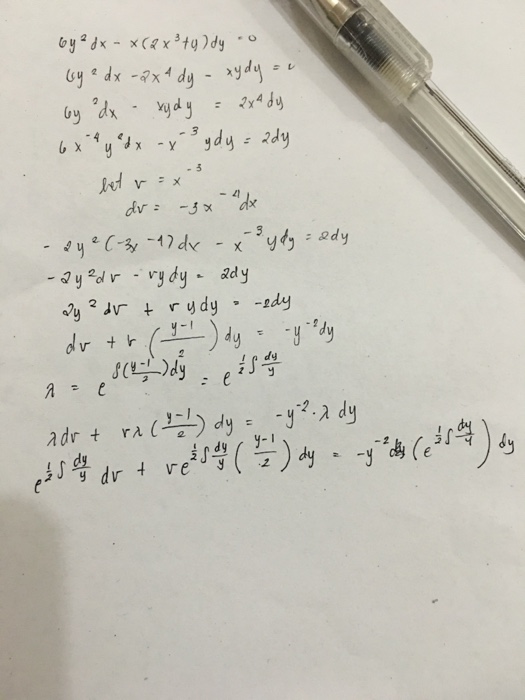



Bernoulli S Equation 6y 2 Dx X 2x 3 Y Dy 0 Chegg Com




Math 432 Hw 2 5 Solutions Pdf Free Download



Solve 1 X 2 Dy Dx Xy Xy 2 Sarthaks Econnect Largest Online Education Community




Solve Y 1 Xy Dx X 1 Xy X 2y 2 Dy 0 Mathematics Stack Exchange




1 X 2 1 Y Dx X Y 1 Y Dy Y 4 1 X 1 Y Dx Xy 1 Y Dy Youtube




Math 432 Hw 2 5 Solutions




Dy Dx 2xy F X Y 0 2 Novocom Top




Y 2 X 2 Dy Dx Xy Dy Dx Youtube



Differential Equation Help D2jsp Topic
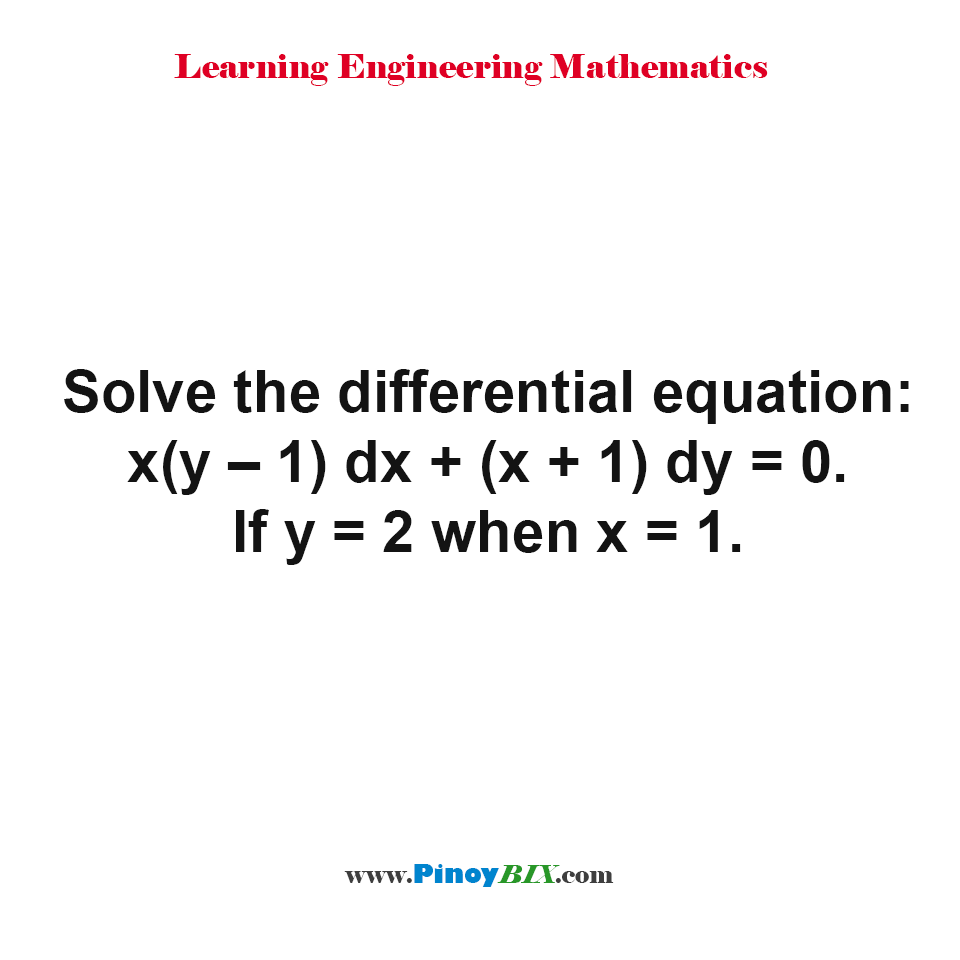



Solution Solve The Differential Equation X Y 1 Dx X 1 Dy 0 If Y 2 When X 1



Find The General Solution Of Y2dx X2 Xy Y2 Dy 0 Studyrankersonline




Dy Dx X Y 1 X Y 3 Novocom Top




Ejercicios Propuestos Ecuaciones Diferenciales Primer Orden Pdf Differential Equations Equations
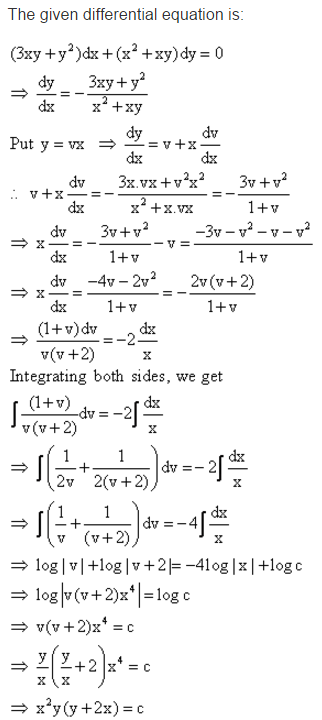



Find The Particular Solution Of Given Differential Equation 3xy Y 2 Dx X 2 Xy Dy 0 At X 1 Y 1 Mathematics Topperlearning Com D1ksg633




Misc 7 Show That General Solution Is X Y 1 A 1 X Y 2xy




Ex 9 5 4 Show Homogeneous X2 Y2 Dx 2xy Dy 0 Ex 9 5
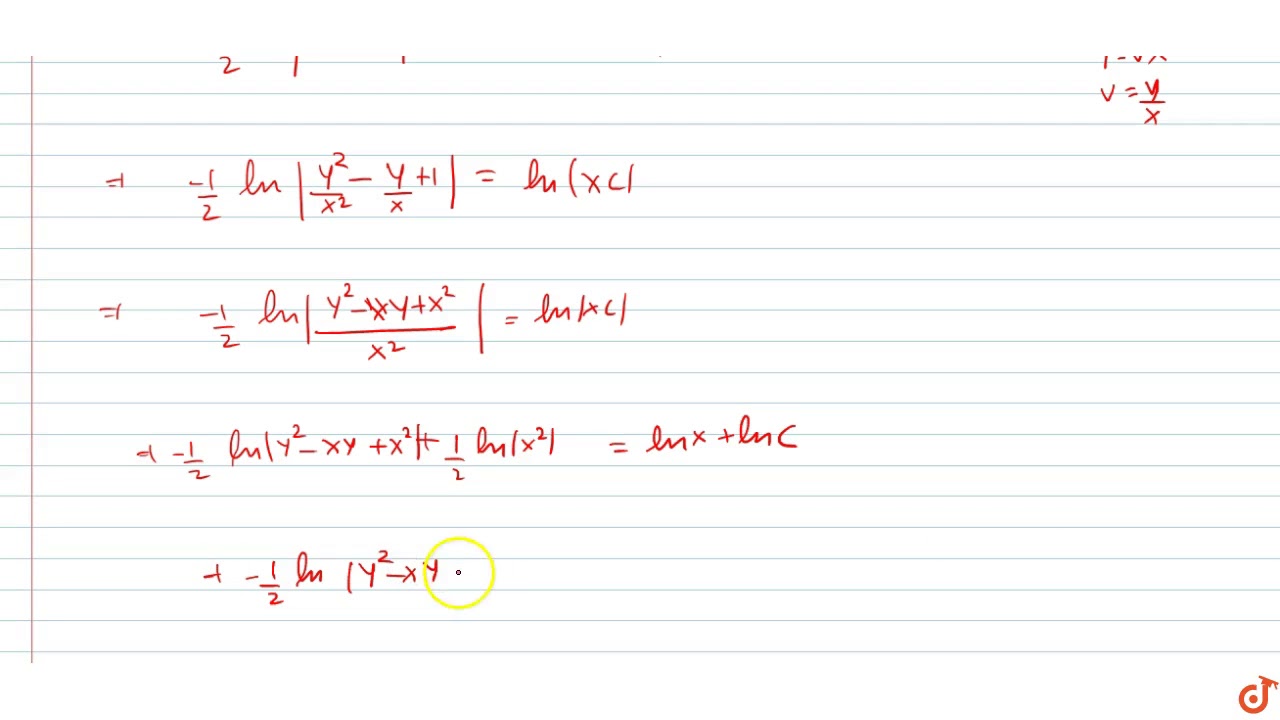



2x Y 1 Dx 2y X 1 Dy 0 Youtube



Solve The Differential Equation Xy 2 X Dx X 2y Y Dy 0 Sarthaks Econnect Largest Online Education Community




Solve Y 2 2x 2y Dx 2x 3 Xy Dy 0 Mathematics Stack Exchange



0 件のコメント:
コメントを投稿